以下是半导体产品可靠性相关的常见术语：

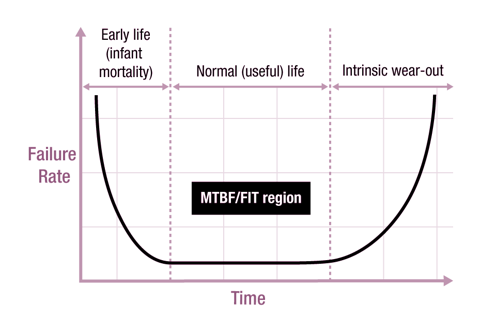
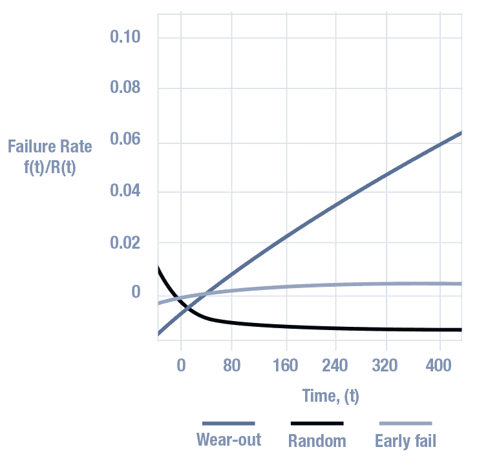
浴盆曲线

浴盆曲线通常用作一个可视化模型来说明产品故障率的三个关键时期，并未经校准以描绘特定产品系列的预期行为。我们通常无法获得足够的短期和长期故障信息来使用经过校准的浴盆曲线对大量产品准确建模，因此一般使用可靠性建模进行估算。

半导体产品寿命有三个主要阶段：

早期故障率（或婴儿死亡率）：此阶段的特点是初始故障率较高，后期将迅速降低。

正常生命期：此阶段的故障率在整个器件有用寿命期间都保持稳定。 此故障率以“FIT”的单位表示，或作为“故障间隔平均时间”(MTBF)，以小时为单位。

劣化阶段：此阶段表示固有劣化机制开始占主导地位并且故障率开始呈几何级增长的时间点。 产品寿命通常定义为从初始生产一直到出现劣化的时间周期。

故障率术语

对于给定的样本大小 n，将在 t 小时

运行之后出现 m 次故障 – 如果在记下故障数“m”之前“n”运行了“t”小时，那么

操作数小时公式

λavg – 平均故障率

平均故障率

FIT - 时基故障，每工作 10 亿个小时发生故障的器件数。您可以使用 TI 的可靠性估算器获取大多数 TI 器件的 FIT 率。

时基故障公式

DPPM – 每百万缺陷器件数，也称为每百万发货量次品数。

每百万缺陷器件公式

MTTF（平均故障时间）= (t1+t2+t3+….tm)/m

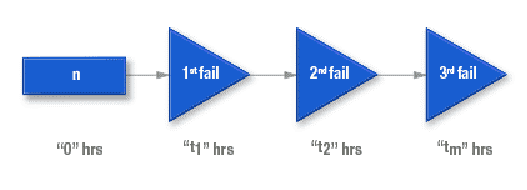
这是发生故障的平均时间。MTTF 用于不可修复系统的情况。

T50（中位故障时间）= 50% 部件发生故障的时间。

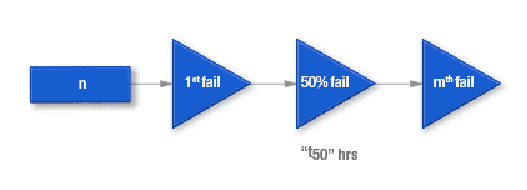
一半故障在 T50 之前发生；另一半在 T50 之后发生。在故障分布的统计处理中常常用到。如果失效时间是正态分布，则 T50 与 MTTF 相同。

       MTBF（故障间隔平均时间）= [t1 + (t2- t1) + (t3 – t2) ….(tm – tm-1) ]/m = tm/m

MTBF 是相继发生的故障之间的平均时间。MTBF 用于可修复系统的情况。它其实是故障间的平均正常运行时间，因为它不含修复时间。

概率分布

概率分布是部件随时间发生故障的比例的图形或数学表示。对于有限的离散故障样本，该分布通常显示为直方图。此分布的曲线形状在数学上用概率分布函数 (PDF) 表示。

概率密度函数 f(t)：

该函数将特定时间 t 的故障概率表示为 f(t).Δt

区域 f(t).Δt 也可以预测特定时间 t 的预期故障数。

累积分布函数 F(t)：

它表示一直到给定时间“t”的累积故障数。

累积分布公式

故障率或风险率 l(t)

故障率是在时间 t 的条件故障概率，即部件能存活到给定时间 t 时的故障概率。

它还可以表示为在 t 和 t+ΔT 之间的时间间隔期间每单位时间发生故障的部件数，以及占存活到时间 t 的部件的比例。

如该图中所示，故障率随时间的变化开始在产品的早期很高，然后快速下降。在有效寿命阶段，故障率是恒定的。随着材料退化并达到劣化，故障率将随时间不断增加。

可靠性函数 R(t)

存活到时间 t 的可能性。它也可以使用另一种方法表示，即存活到时间 t 的部件的比例。

发生故障和存活的总比例之和必须为 1。

R(T) + F(T) = 1

根据前所述的 f(t)、F(t)、R(t) 和 l(t) 的定义

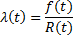
当故障率 l(t) 为常量时，可靠性函数呈指数分布  

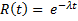
对于恒定的故障率（即浴盆曲线的正常运行部分），指数分布对于为故障概率和寿命建模而言很有用。

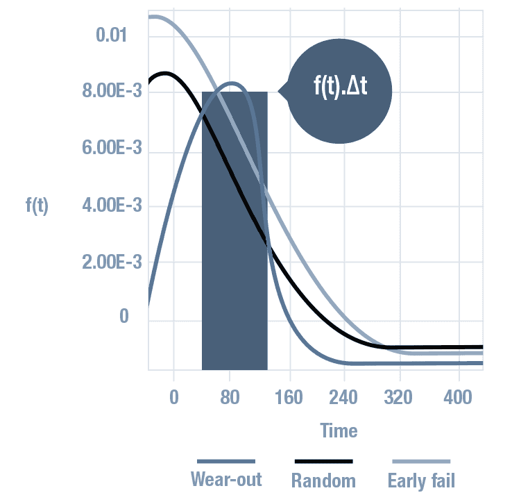
威布尔分布

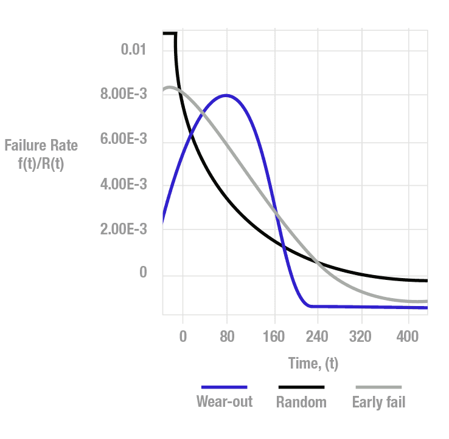
威布尔分布是由 Waloddi Weibull 创造的连续概率分布。在可靠性中，它用于时变故障率。 在实践中，故障概率通过 3 参数威布尔分布进行建模：

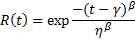
η、β、γ 是由应力测试故障部件确定的参数。

在很多情况下，只有两个参数是可靠性建模必需的，因此威布尔分布简化为：

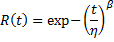
β 称为“威布尔斜率”，η 称为分布的“特征寿命”。

浴盆曲线的三个部分 – 早期故障、有效寿命和劣化 – 常具有不同的故障分布形状，如图所示。

威布尔分布是功能强大的数学函数，可以表示浴盆曲线的所有三个阶段，通常只需使用两个可调参数 – β 和 η。

它常常用于可靠性建模。